- About Us
About RSIS International
Publication Method
Conference
Contact Us
- Journals
- Conference Proceedings
Days
Hours
Minutes
Seconds
Submission Deadline
The International Journal of Latest Technology in Engineering, Management & Applied Science (IJLTEMAS) is an open-access platform committed to promoting advancements in engineering, management, and applied sciences. We facilitate scholarly communication by providing a multidisciplinary forum for researchers, practitioners, and scholars to exchange innovative ideas and findings. Our journal aims to bridge the gap between theory and practice, encouraging the dissemination of high-quality research that contributes to the technological and managerial landscape.
Affordable Publication Fee
Open Access for All
Years of Publishing Excellence
Reviewers from 71+ Countries
Countries Global Authorship
Share your groundbreaking research with an international audience
Be featured in the next edition!
The International Journal of Latest Technology in Engineering, Management & Applied Science (IJLTEMAS) is an open-access platform committed to promoting advancements in engineering, management, and applied sciences. We facilitate scholarly communication by providing a multidisciplinary forum for researchers, practitioners, and scholars to exchange innovative ideas and findings. Our journal aims to bridge the gap between theory and practice, encouraging the dissemination of high-quality research that contributes to the technological and managerial landscape.
Affordable Publication Fee
Open Access for All
Years of Publishing Excellence
Reviewers from 71+ Countries
Countries Global Authorship
Share your groundbreaking research with an international audience
Be featured in the next edition!
We are now accepting submissions for the next issue of 2025. This is your opportunity to contribute to the year’s concluding edition and showcase your research to a global audience.
The International Journal of Latest Technology in Engineering, Management & Applied Science (IJLTEMAS) invites authors, scholars, researchers, and academicians to submit original, high-quality research papers, review articles, case studies, technical reports, dissertations, and research proposals. We welcome contributions that address the latest trends, innovations, and practical applications in engineering, management, and applied sciences.
The International Journal of Latest Technology in Engineering, Management & Applied Science (IJLTEMAS) aims to provide an accessible, high-quality platform for the dissemination of peer-reviewed research that fosters advancements in technology, management, and applied sciences. Our mission.
The Engineering section of IJLTEMAS provides a dynamic platform for researchers, engineers, and academicians to share groundbreaking research, innovative solutions, and technical advancements across various engineering disciplines. Our open-access model ensures that valuable knowledge reaches a global audience, fostering collaborative growth and development.
The Management section of IJLTEMAS provides a platform for researchers, scholars, and professionals to share innovative ideas, empirical research, and practical insights in various areas of management. We aim to bridge the gap between theory and practice, promoting knowledge that supports business excellence, strategic decision-making, and sustainable growth.
The Applied Science section of IJLTEMAS serves as a multidisciplinary platform for scientists, researchers, and practitioners to present innovative research and practical applications of scientific principles. We focus on research that bridges theory with real-world applications, driving advancements across industries and contributing to societal progress.

At the International Journal of Latest Technology in Engineering, Management & Applied Science (IJLTEMAS), we are committed to providing a platform that fosters academic freedom and encourages the dissemination of knowledge. Our Open Access policy ensures that all published research is freely available to readers worldwide, promoting greater visibility and accessibility of scholarly work.










Authors submit their manuscripts for review.
Expert reviewers evaluate the paper for quality and relevance, and the editorial team takes the final decision based on their feedback.
Authors receive feedback, which can be either accepted for publication, require revisions, or be rejected.
Proceed for Final Submission
For accepted papers, authors submit the Author Declaration form, pay registration fees, and make any required revisions if necessary.
The accepted paper is published online, making it accessible to the public.
Structure Your Paper: Organize your research into a clear structure, typically including an abstract, introduction, methods, results, discussion, and references.
Follow Formatting Guidelines: Adhere to the journal’s formatting requirements, including citation style, word count, and figure/table formats.
Edit and Proofread: Review your manuscript for clarity, coherence, and grammatical accuracy. Consider seeking feedback from colleagues or mentors.
Online Submission System: We accept submission through an online portal.
Format: Ensure your paper is submitted in an allowed format (e.g., DOC, DOCX, or RTF).
Initial Review: After submission, your manuscript will undergo an initial review by the editorial team.
Peer Review: If deemed suitable, your paper will be sent to peer reviewers who will evaluate its quality and validity. Be prepared for constructive feedback.
Accepted: If your manuscript is accepted, you will receive a formal acceptance notification from the journal.
Revision Required: If revisions are requested, address the reviewers’ comments carefully. Provide a detailed response to each point raised and resubmit your revised paper, including a cover letter that outlines how you addressed the feedback.
Rejected: If your manuscript is rejected, take the opportunity to review the feedback provided. Consider revising your work based on the comments and reapplying to the same one in the future.
Acceptance Notification: If your manuscript is accepted, you will receive a formal acceptance notification from the journal.
Author Declaration: Send a scanned copy of the author declaration form.
Final Paper Submission: Submit the final version of your paper and pay required registration fees.
Publication: Your paper will be published online on the journal’s website, making it accessible to the academic community and the public.
Publication Certificate: You will receive a publication certificate for all authors, confirming the successful publication of the paper.
Share Your Research: Promote your published work through social media and academic networks to increase visibility and impact.
The initial submission marks the first step in the publication process. We invite you to submit your research now.
Final step toward publication: submit the author declaration, final paper, and complete the registration process.
We invite submissions that address a wide range of topics, including but not limited to.
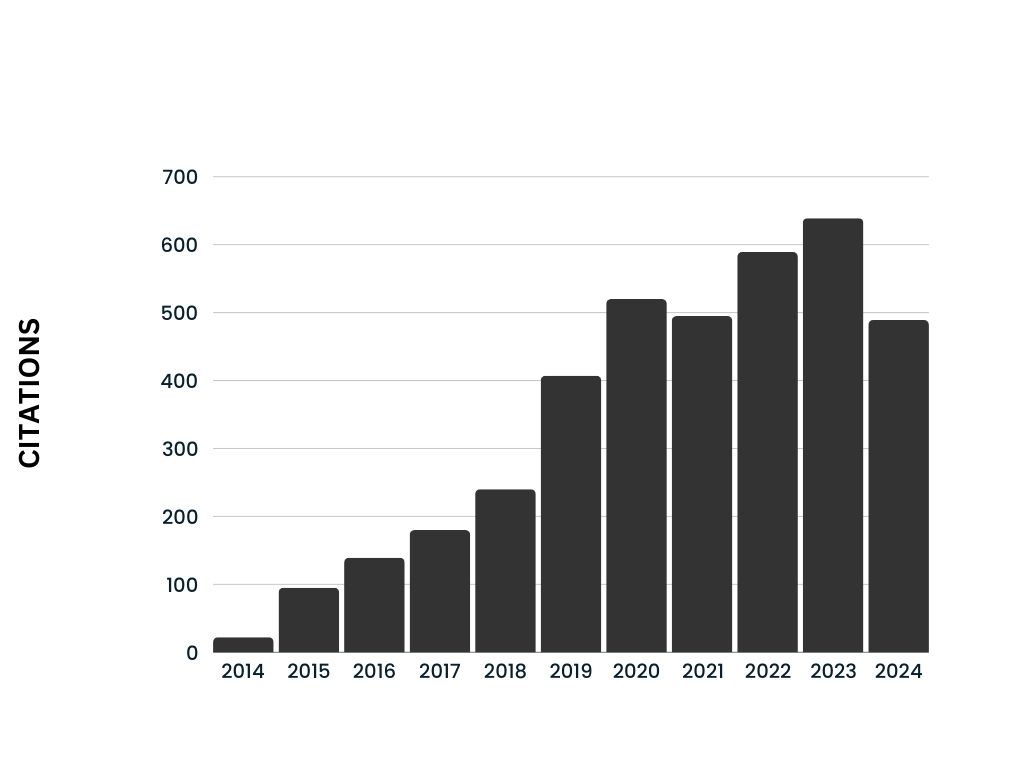
126 ( Total)
Citations
H-Index
i10-Index

Romania
Professor, Hyperion University, Bucharest, Romania

Indonesia
Associate Professor

Indonesia
Lecturer

Philippines
BSCpE Program Adviser, Research Coordinator
Indexing And Abstracting
Indexing And Abstracting
Indexing And Abstracting
Indexing And Abstracting
Indexing And Abstracting
Indexing And Abstracting
Indexing And Abstracting

Open Access for All
Empowering Knowledge Sharing with 100% Open Access for All

Years of Publishing Excellence
Over a Decade of Trusted Knowledge Dissemination

Reviewers from 71+ Countries
A Worldwide Network of Expert Reviewers from Diverse Countries

Countries Global Authorship
A Global Overview of Authorship Trends Across Countries
Welcome to the Engineering, Management & Applied Science Journal —a leading peer-reviewed (refereed), open-access journal dedicated to publishing high-quality research in the fields of engineering, management, and applied sciences.
✅ Peer-Reviewed (Refereed) Journal – Every submission undergoes a double-blind peer-review process, ensuring research quality and credibility.
✅ Rapid & Rigorous Review – Papers are reviewed within 2-4 weeks by subject matter experts.
✅ Indexed & Globally Recognized – Listed in various academic databases for maximum visibility.
✅ Affordable Open-Access Model – We charge a nominal fee to keep publishing accessible to all researchers.
✅ Experienced Editorial Board – Our board consists of renowned scientists, academicians, and industry professionals.